Problèmes

Etant donné trois nombres positifs a, b et c, démontrer que :

Existe-t-il un réel positif a  tel que : " n Î N : [ a [ (a + 1)n ] ] = n - 1 ?

(en notant [ x ] la partie entière de x, le plus grand entier inférieur ou égal à x, que l'on note également E(x)).

Déterminer tous les triangles ABC vérifiant la propriété suivante : la médiatrice de [BC], la hauteur issue de B et la bissectrice intérieure issue de C sont concourante.

Soit E = { 1, 2, ..., 25 }. Montrer que tout sous-ensemble F de E d'au moins 17 éléments contient deux entiers dont le produit est un carré parfait.

Montrer qu'il existe deux entier naturels a et b tels que 2^a - 2^b soit divisible par 1999.

Thérèse a calculé les carrés de 52 nombres entiers. Montrer qu'elle peut toujours choisir, parmi ces carrés, 2 nombres dont la différence est divisible par 100.

Soit un triangle ABC et A', B' et C' les symétriques respectifs de A, B et C par rapport a (BC), (CA) et (AB). Trouver une condition pour que A', B' et C' soient alignés.

Six figures : un cercle, un triangle, un carré, un trapèze, un pentagone et un hexagone ont été coloriées sur un tableau dans six couleurs différentes. On demande le lendemain leurs couleurs à deux élèves.

Alexandre :  " Un cercle rouge, un triangle bleu, un carré blanc, un trapèze vert, un pentagone rose et un hexagone jaune. "

Bénédicte :  " Un cercle jaune, un triangle vert, un carré rouge, un trapèze bleu, un pentagone rose et un hexagone blanc. "

En réalité, Alexandre s’est trompé trois fois, Bénédicte deux fois.

Quelle était la couleur de chacune des six figures géométriques ?

Trois vacanciers Christophe, Denise et Eric partagent un chalet. Pour cuisiner, ils disposent d'un poêle à bois et chacun doit fournir ses bûches. Christophe en apporte cinq et Denise trois. Eric, lui, qui n'avait pas de bois, a obtenu des deux autres la permission de préparer son déjeuner sur le poêle. A titre de compensation, il leur a versé 8 euros. Comment Christophe et Denise doivent-ils se partager cette somme (pour que le partage soit équitable) ?

Florence et Guillaume ont été invité à une cérémonie réservée aux couples mariés. Celle-ci comporte 100 couples, tous mariés, qui se connaissent plus ou moins. Guillaume, fin observateur, a remarqué que beaucoup de poignées de mains ont été échangées. Passionné de statistiques, il décide alors de demander à toutes les personnes présentes combien de mains elles ont serré en entrant (on ne compte pas les mains serrées en partant, d'ailleurs, personne n'est parti !). Ce nombre est bien sûr très variable et dépend de la personnalité de chacun. Curieusement, il obtient des réponses toutes différentes. Pouvez-vous en déduire le nombre de mains serrées par Florence, la femme de Guillaume ? Inutile de le dire à Guillaume qui, lui, le sait (il l'a demandé à sa femme)

Hélène a fait un gâteau en forme de quadrilatère. Ivan le partage en quatre parts en reliant les sommets opposés. Julie trouvant que ce gâteau avait une forme peu courante voulu calculer sa surface lorsque Kevin sans plus attendre, prit une part et la mangea aussitôt empêchant ainsi Julie d'effectuer son calcul.

Ivan la réconforta en lui disant : "Ce n'est pas grave, on va quand même pouvoir calculer l'aire de ce gâteau".

En effet, après avoir trouvé que les trois parts restantes avaient pour surface 80, 120 et 150 cm², ils purent déterminer la surface du gâteau. Quelle est donc la surface de ce gâteau ?

P.S. : Bien sûr, Kevin a prit la part la plus grosse.

Trois amis, , , et étaient d'excellents logiciens, et chacun savait que les autres l'étaient. L'art du raisonnement n'avait pas de secret pour eux et ils trouvaient instantanément toutes les énigmes. Un jour, pour les mettre à l'épreuve, on leur montra 7 rubans : 2 rouges, 2 jaunes et 3 verts, puis on leur banda les yeux. Pendant qu'ils étaient ainsi on fixa un ruban sur chacun de leurs chapeaux, puis on cacha les quatre rubans restants. Ensuite, après les avoir débarrassés de leurs bandeaux, on leur demanda : " Pouvez-vous dire de façon certaine une couleur qui ne soit pas celle de votre ruban ? "

D'abord répondit non, puis dit non à son tour.

Sans en savoir plus, pouvez-vous retrouver la couleur des rubans de , et ?

Dans l'énigme précédente les prénoms des trois amis ont été cachés. Pouvez-vous retrouver ces trois prénoms ?

Bien qu'il y ait plusieurs solutions, ceux-ci suivent une certaine logique. La retrouverez-vous ?

Oscar a été capturé par les terribles Logicos, qui veulent tester son raisonnement. Il est enfermé dans une salle dont la porte s'ouvre grâce au système suivant :

32 cadrans circulaires tricolores, ne pouvant tourner que dans le sens des aiguilles d'une montre, sont placés "rouge en bas". La porte ne peut s'ouvrir que si les 32 cadrans sont placés "blanc en bas".

Mais la manipulation des disques est soumise aux conditions suivantes :

- On doit, à chaque "coup", tourner cinq cadrans à la fois, ces cadrans pouvant être ou ne pas être consécutifs.

- Chaque cadran ne peut tourner que d'un tiers de tour à chaque "coup".

Dès que l'une de ces conditions est transgressée, la porte devient irrémédiablement bloquée.

Quel est le nombre minimum de coups nécessaires à Oscar pour ouvrir la porte ?

Patricia a cassé ses deux colliers de perles. De celui en perles véritables, sept se sont détachées. De celui en fausses perles, une seule s'est détachée. Les huit perles sont identiques en apparence, la fausse est seulement un peu plus légère que les autres. Comment l'identifier en deux pesées avec une simple balance non graduée ?

Pouvez-vous aider Quentin à remettre les livres de son étagère dans le bon ordre ?

Attention, vous n'avez le droit de déplacer que 3 groupes de livres, chaque déplacement consistant à prendre un certain nombre de livres contigus, et à les placer à côté ou entre d'autres ouvrages.

Rose, Stéphane, Tina et Ulrich ont acheté un ordinateur dans quatre villes de France. Retrouver à l'aide des indices ci-dessous quels sont les processeurs (AMD, Céléron, Pentium II, Pentium III) de leur PC et dans quelles villes (Bordeaux, Marseille, Nantes, Paris) ils ont fait leur achat.

Indice 1 : Rose ne possède pas de Pentium III ni de Céléron.

Indice 2 : Stéphane a acheté un Pentium à Marseille.

Indice 3 : Tina n'a pas acheté son AMD à Paris.

Indice 4 : Le Céléron a été acheté à Bordeaux.

Après s'être assoupis en écoutant le conte de fées lu par leur maman, cinq enfants (Valérie, William, Xavière, Yann et Zoé) ont fait un cauchemar (Dragon, Lutin, Monstre, Ogre et Sorcière) et se sont réveillés en réclamant à boire, un bonbon, des câlins, de la lumière ou un ours en peluche. Retrouvez le prénom des bambins, puis calculez l'heure (21 h 30, 21 h 40, 21 h 50, 22 h, 22 h 10) de chaque réveil brutal.

Pour cela 5 indices :

Indice 1 : Valérie s'est réveillée juste avant celle qui a rêvé d'un lutin et juste après l'enfant qui voulait des bonbons.

Indice 2 : L'enfant qui a voulu que la lumière reste allumée n'a pas rêvé d'un dragon et ne s'est pas réveillé à 21 h 30.

Indice 3 : L'enfant qui a eu droit aux câlins après avoir rêvé d'une sorcière, ne s'est pas réveillé à 22 h 00 et ne s'appelle pas Zoé.

Indice 4 : William a rêvé d'un ogre, qui ne l'a pas réveillé à 21 h 40. Il n'a pas réclamé son nounours.

Indice 5 : Yann, qui s'est réveillé à 21 h 50 n'a pas rêvé d'un dragon.

Le chevalier Arthur s'apprêtait bien imprudemment à pénétrer dans la forêt des mille et un diables, forêt triangulaire redoutable, quand un diablotin l'arrêta :

- N'y pénètre pas si vite! Tu es au sommet A, tu dois aller par le plus court chemin jusqu'au côté BC. Là-bas, un énorme diable te demandera le nombre exact de mètres que tu as parcouru en forêt. Gare à toi si tu l'ignores !

- Encore un renseignement contre ma lance ! dit Arthur.

- Je parle en mètres, reprit le diablotin. Si j'ajoute un au grand côté de la forêt, je trouve le même nombre qu'en multipliant par trois la différence entre le petit côté et onze. Si j'ajoute un au côté intermédiaire, j'obtiens les vingt-cinq neuvièmes du petit côté.

- Ce n'est pas suffisant, grogna Arthur, va pour mon cheval !

- Bien : si chaque côté de la forêt était augmenté d'un nombres de mètres égal à mon année de naissance, le nouveau périmètre serait de 10500 m.

- Mon épée contre ton année de naissance, implora Arthur.

- Eh bien, sache que je suis né au vingtième siècle, et que mon année de naissance est égale à la différence de deux cubes d'entiers impairs consécutifs !

Arthur partit alors à pied, et traversa la forêt.

Quelle réponse a-t-il donné au gros diable ? (on arrondira au mètre le plus proche).

On écrit la liste des nombres qui s'écrivent avec les chiffres 1, 2, 3, 4, 5, 6, 7, 8 et 9, chacun pris une seule fois. On les classe dans l'ordre croissant : Il y en a 362880 (Si, je les ai comptés !), qui vont du premier 123456789 au dernier 987654321. Mais quel est le 100000^ème ?

En laissant tomber un cube dans du sable, on s'aperçoit que la trace laissée sur le sol peut être un triangle, un rectangle, un pentagone ou un hexagone. Si on obtient un triangle équilatéral dont un côté mesure 10 cm, pouvez-vous dire à quelle profondeur le cube s'est enfoncé ?

Ma fille (10 mois) possède un boulier que l'on attache à sa poussette. Celui-ci est constitué de 2 boules bleues identiques, de 2 poissons rouges identiques et d'un poisson jaune.

A force de tirer dessus, elle a réussit à casser l'élastique qui tenait le tout et les cinq éléments se sont mélangés.

Ne me souvenant plus de la position initiale des cinq objets, j'aurais voulu savoir combien de possibilités s'offrent à moi pour reconstruire son boulier.

Attention à ne pas en oublier !

Les deux bouliers suivants sont différents :

Mais les deux suivants sont identiques (il suffit de regarder le boulier "de derrière") :

Si on place deux points sur un cercle, on crée deux régions en reliant les deux points.

Si on place trois points sur ce cercle, on crée en reliant les points de toutes les manières possibles, quatre régions.

Quel est le nombre maximal de régions créées lorsqu'on place dix points sur le cercle ?

Par exemple, avec 4 points, on obtient 8 régions :

Peut-on découper un carré en 12 carrés et combien y a-t-il de façons de réaliser ce découpage? (on ne s'intéresse qu'aux 12 morceaux et non à leur place initiale.)

Les côtés des petits carrés et celui du grand carré sont "commensurables". On peut donc ne considérer que des longueurs entières.

Un découpage est de base n signifie : le PGCD des longueurs des côtés des 12 petits carrés est 1 et la longueur du côté du grand est n.

Soit 2 cercles tangents en A et d leur diamètre commun. Construire un cercle tangent à ces 3 courbes.

Le lavoir municipal est équipé de 3 robinets. Si l'on n'ouvre simultanément que le premier et le deuxième robinet, le bac du lavoir se remplit en 1 h 10 m. Si l'on n'ouvre simultanément que le premier et le troisième robinet, le bac se remplit en 0 h 50 m. Si l'on n'ouvre simultanément que le deuxième et le troisième robinet, le bac se remplit en 0 h 56 m.
Si l'on ouvre simultanément les 3 robinets, en combien de temps le bac sera-t-il remplit ?

Pour établir les neuf égalités demandées, il faut : N'utiliser que des "1" dans la première ligne, des "2" dans la deuxième ligne..........des "9" dans la neuvième ligne. Utiliser 6 fois le même chiffre dans la même égalité.

N'utiliser que les quatre opérations (+, -, x, :) et la racine carrée.

1) 21 = 11+11- 1/1 ....................

2) 21 = ............................

3) 21 = ............................

4) 21 = ......................................

5) 21 = .............................

6) 21 = ............................

7) 21 = ......................................

8) 21 = .............................

9) 21 = ............................

Pour faire une pyramide classique (3 faces) de billes à 4 étages, il faut 20 billes. Sachant que les billes font 2 cm de diamètre, quelle est la hauteur de la pyramide ?

Un élastique est tendu entre un point fixe A et un point mobile B distants de 12 cm. Une fourmi part du point A vers le point B à la vitesse de 4 cm à la minute, sachant que l'élastique est étiré de 3 cm à la fin de chaque minute, en combien de temps la fourmi sera rendue en B ?

Quatre fontaines (A, B, C, D) alimentent un bassin, la fontaine A remplit le bassin en 2 jours, tandis qu'il faut 3 jours à la B, 4 jours à la C et 1 jour à la D. Sachant que le bassin s'évapore en 20 jours lorsqu'il n'est pas alimenté, combien de temps faut-il aux quatre fontaines ensemble pour remplir le bassin ?

Une fermière ne possédant pas d'argent liquide règle une dette en donnant une vache, un veau, un cochon et un poulet. Elle avait payé 108210 F pour cinq vaches, sept veaux, neuf cochons et un poulet. Une vache vaut 4000 F de plus qu'un veau, trois veaux autant que dix cochons et trois mille poulets autant que cinq veaux. Combien a-t-elle payé pour régler sa dette ?

Pour remplir une cuve cylindrique, on dispose de plusieurs tuyaux d'arrivée, tous de même débit ; ces tuyaux sont ouverts progressivement l'un après l'autre. Au départ un seul est ouvert. Lorsqu'un certain niveau est atteint, le second tuyau se met en marche automatiquement, etc. Un détecteur de niveau est placé tous les 40 cm le long de la paroi de la cuve, à partir du fond. Le premier détecteur est atteint au bout de 20 minutes. 50 minutes après l'ouverture du premier tuyau le mécanisme s'arrête. Le niveau de l'eau dans la cuve se trouve alors à 16 cm du bord. Quelle est la hauteur de la cuve ?

S'il écrit son âge 3 fois à la suite, Théodore retrouve le produit de son âge par celui de sa femme et par ceux de leurs quatre enfants. S'il écrit son âge 4 fois à la suite, il retrouve le produit de son âge par ceux de son père, son grand-père et son arrière-grand père, s'ils étaient encore vivants. D'autre part, il constate que son âge est le quart de la différence de l'âge qu'aurait son arrière-grand-père et celui de son plus jeune enfant. Quel est donc l'âge de Théodore ?

64 allumettes sont disposées sur une table en 4 tas inégaux. Si l'on transfère du premier tas au troisième autant d'allumettes qu'il y en a dans le deuxième, du quatrième au deuxième autant qu'il y en a dans le deuxième, du premier au troisième autant qu'il y en a alors dans le troisième, et enfin du troisième au quatrième autant qu'il y en a alors dans le quatrième, on obtient un nombre identique dans tous les tas. Combien y avait-il d'allumettes au départ dans chacun des tas ?

Des abeilles, en nombre égal à la racine carrée de la moitié de l'essaim, se sont posées sur un arbre de jasmin, laissant derrière elles les 8/9 de l'essaim. Une seule abeille du même essaim tournait autour d'un lotus, attirée par le bourdonnement d'une amie tombée par mégarde dans le guet-apens de la fleur au parfum subtil. Combien d'abeilles y avait-il dans l'essaim ?

Sur la tombe de Diophante (mathématicien grec du IIIè siècle) est écrit ceci : les chiffres diront la durée de sa vie. Sa douce enfance en fait le sixième, un douzième de sa vie a passé. Marié il a vécu le septième de sa vie sans enfant. Cinq ans ont passé. La naissance d'un fils l'a rendu heureux. La vie de ce fils fut deux fois plus courte que celle de son père. Le vieillard a rendu l'âme quatre ans après la mort de son fils. A quel âge est mort Diophante ?

Jean dit un jour à Paul : "Je suis trois fois plus âgé que vous ne l'étiez lorsque j'avais l'âge que vous avez aujourd'hui." Et Paul répondit "Quand j'aurai l'âge que vous avez aujourd'hui, le total de nos âges sera de 77 ans." Quel est l'âge de Jean et celui de Paul ?

Chez le poissonnier, j'ai observé trois clientes qui achetaient les mêmes espèces de poissons. La première a acheté 2 limandes, 5 maquereaux, 4 carrelets et a payé 62 F. La seconde, 3 limandes, 5 maquereaux, 1 carrelet et a payé 53 F. La troisième, 2 limandes, 7 maquereaux et 8 carrelets. Combien cette dernière a-t-elle dépensé ?

Un nombre de trois chiffres augmente de 45 si l'on intervertit l'ordre des deux chiffres de droite, et il diminue de 270 si l'on intervertit l'ordre des deux chiffres de gauche. Que devient-il si l'on intervertit l'ordre des deux chiffres extrêmes ?

75 vaches ont brouté en 12 jours l'herbe d'un pré de 60 ares. 81 vaches ont brouté en 15 jours celle d'un pré de 72 ares.

Combien de vaches un pré de 96 ares pourra-t-il nourrir pendant 18 jours ?

Un marchand a vendu à son premier client la moitié de ses pommes plus une 1/2 pomme, au deuxième client la moitié du reste plus une 1/2 pomme, au troisième client, la moitié du reste plus une 1/2 pomme, etc. …, jusqu'au septième client, après lequel il ne lui restait plus de pommes. Combien de pommes avait le marchand ?

Un maire dit à son secrétaire : "J'ai vu aujourd'hui trois personnes. Le produit de leurs âges est 2 450. Peux-tu me dire leurs âges respectifs ?" Le secrétaire répondit non. Le maire dit :"Je précise que la somme de leurs âges est le double du tien, peux-tu me répondre ?"
Pas encore dit le secrétaire. Le maire dit :" J'ajoute que la plus âgée est plus âgée que moi." Maintenant j'en sais assez répondit le secrétaire. Pouvez-vous comme le secrétaire trouver les âges des trois personnes ?

Les bergers Luc et Max marchent vers le Nord à la recherche de nouveaux pâturages. Ils marchent trois jours, mais pas à la même allure. Le premier jour le chemin de Max est les 9/11 de celui de Luc, le deuxième jour les 11/9, et, le troisième jour les 33/11. Par ailleurs, les hommes se fatiguent, de sorte que la somme des trajets du troisième jour est de 20% inférieure à celle du deuxième jour elle même inférieure de 20% à celle du premier jour. Dans ces conditions, qui de Luc ou de Max alla le plus loin ?

Je ne vous direz pas mon âge, dit Monsieur Beliot, professeur de mathématiques, mais vous le calculerez aisément quand je vous aurai dit que c'est un nombre impair dont le carré est formé de trois chiffres dont les deux premiers sont le palindrome (nombre inversé) de mon âge, et le dernier (celui des unités) donne le total des deux chiffres de mon âge. Quel âge a donc monsieur Beliot ?

Voilà qui est surprenant ! dit Michel. Quand j'atteindrai un âge correspondant au palindrome (âge inversé) de mon âge actuel le carré de mon âge sera alors le palindrome du carré de mon âge actuel. Vous trouverez facilement mon âge quand je vous aurai dit que cette particularité se répétera l'an prochain, et que le carré de mon âge est formé de trois chiffres. Quel est l'âge de Michel ?

Comme c'est bizarre ! dit Ernest. Quand j'aurai trois fois mon âge actuel, le carré de mon âge sera le palindrome du carré de mon âge actuel, carré qui est un nombre de quatre chiffres différents. Quel est l'âge d'Ernest ?

C'est amusant ! dit Alphonse, j'ai deux fois l'âge de mon frère et cinq fois l'âge de ma sœur. Ma mère a trois fois mon âge. Ma grand-mère a deux fois l'âge de ma mère et mon grand-père a deux fois l'âge de mon père. Si on multiplie mon âge à ceux de mes parents, grands-parents, frère et sœur, on obtient le nombre 441 suivi de six zéros. Quel est l'âge d'Alphonse ?

Vous trouverez mon âge, dit Antoine, quand je vous aurai dit qu'il suffit de l'ajouter à son carré pour obtenir un nombre terminé par deux zéros, et dont les deux premiers chiffres représentent le palindrome de mon âge. Quel âge a Antoine ?

Un nénuphar double de surface chaque jour. Il a mis 33 jours 19 heures 35 minutes et 28 secondes pour recouvrir la surface d'un étang. Pour recouvrir le même étang (et sans se recouvrir entre eux), combien de temps mettront deux nénuphars ?

Un cylindre de verre a une hauteur de 200 mm et une circonférence de 300 mm. A l'intérieur et à 50 mm du sommet se trouve une goutte de miel. Une mouche est située à l'extérieur du cylindre, plus précisément à 50 mm de sa base, du côté directement opposé au miel. Quel est le chemin le plus court que doit emprunter la mouche pour atteindre le miel en marchant et la distance exacte que cela représente ? (oubliez l'épaisseur du cylindre)

Pour 36 F, une cliente a acheté au marchand de légumes 1 kg d'aubergines, 1 kg de haricots verts, 1 kg de tomates et 1 kg d'asperges. En ajoutant 2 F au prix des aubergines, en retirant 2 F au prix des haricots verts, en doublant le prix des tomates et en divisant par deux le prix des asperges, on obtiendrait le même prix pour chaque variété de légumes. Quels étaient les prix des différents légumes ?

L'armée du général Lee marchait d'un pas paisible et s'étirait sur dix kilomètres. Lee n'était pas tranquille, car il devait traverser un défilé dans lequel il avait perdu ses trois précédentes armées. Aussi avait-il commandé à l'officier placé en serre-file de lui envoyer un message dès que le dernier homme serait sorti du défilé. Tout alla bien cette fois et l'officier envoya un cavalier avertir Lee. Lorsque le cavalier rejoignit l'officier à l'arrière-garde pour lui dire qu'il avait accompli sa mission, celui-ci se trouvait à l'endroit où passait la tête de l'armée lors de son départ. Quelle est la longueur du trajet parcouru par le cavalier ?

Un réservoir a la forme d'un parallélépipède rectangle, dont la largeur est égale à la moitié de la longueur. Il est rempli aux trois huitièmes de sa hauteur. En rajoutant 76 hl, le niveau monte de 0,38 mètre. Il reste alors les deux septièmes du réservoir à remplir. Quelle est la hauteur du réservoir ?

Au cours d'une soirée, des amis échangent tous des poignées de mains. Pendant la soirée, quelques amis s'en vont discrètement un à un. A la fin de la soirée, les amis restant, avant de se quitter, se serrent la main une deuxième fois.

Le nombre de poignées de mains a alors diminué de 76 par rapport à la première fois, au début de la soirée.

Combien y avait-il d'amis à cette soirée ?

Un fermier avait calculé que la quantité de grains qu'il possédait suffirait à nourrir ses 75 poulets pendant une certaine période. Malheureusement un renard est venu lui dérober un poulet chaque nuit, de telle sorte qu'il a eu suffisamment de grains pour une période 50% plus longue que celle initialement prévue.

Si le renard n'avait pas mangé de poulets, combien de jours aurait duré la réserve de grain ?

Trouvez deux nombres A et B en tenant compte des données suivantes : Le nombre A comporte trois chiffres. Le chiffre des centaines de ce nombre est égal au tiers du chiffre des unités et le chiffre des dizaines de ce nombre est le double de la somme des deux autres. Le nombre B a quatre chiffres. La somme de ses chiffres est égale à 18. Le chiffre des dizaines est égal à la moitié de celui des unités. Le chiffre des centaines est égal à la somme du chiffre des dizaines et de celui des milliers. Si l'on ajoute 6 903 à ce nombre, on obtient le nombre renversé.

Trois amis, Alain, Frédéric et Daniel, ont fait la tournée des bars. A chaque bar, ils commandaient un petit blanc, un pastis et un whisky, puis le hasard déterminait qui buvait quoi. Chacun payait sa consommation. Alain, qui racontait cette soirée à son épouse, ne se souvenait plus combien de bars ils avaient ainsi visité, à part qu'au dernier bar, il eut droit au whisky. Il avait dépensé 9 F comme Frédéric, Daniel lui, avait payé 22 F. Chaque consommation coûtait un nombre entier de francs, le même dans tous les bars. Le whisky coûtait le plus cher, et le vin blanc le moins.

Combien de bars ont visité les trois amis, et qu'ont-ils bu chacun ?

La durée totale du croisement* du Paris-Bordeaux avec un premier train roulant en sens inverse a été de 10 secondes. Quelques minutes plus tard, le Paris-Bordeaux rencontre un second train ; la durée totale de ce second croisement est de 8 secondes. Plus tard, ce deuxième train rattrape le premier. Ils sont alors sur deux voies parallèles Les trois trains sont tous de même longueur et chacun d'eux roule à vitesse constante durant cette période.

Quelle sera la durée totale du dépassement du premier train par le second ?

*La durée totale d'un croisement est celle qui s'écoule entre l'instant où les deux têtes de train sont au même niveau et celui où les arrières le sont aussi. Par analogie, la durée totale d'un dépassement est celle qui s'écoule entre l'instant où l'avant du train le plus rapide coïncide avec l'arrière de l'autre train et celui où l'arrière du train le plus rapide arrive au niveau de l'avant de l'autre train.

Comment obtenir 1, en utilisant une fois et une seule chacun des dix chiffres de 0 à 9 et en ne faisant intervenir que des opérations élémentaires ? Comment obtenir 100 de la même manière ?

Nicolas habite en A près d'un jardin carré de 40 m de côté. Chaque matin, en allant en B chercher son journal, il voit Nestor habitant C traverser le jardin pour aller en D acheter son pain. Lorsqu'ils sortent en même temps de chez eux, ils sont de retour également chez eux en même temps.

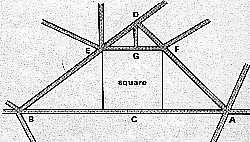
Aujourd'hui, Nicolas a quitté sa maison à l'instant même où Nestor ouvrait la grille du jardin en G pour se rendre à la boulangerie. Il remarqua que Nestor rentrait chez lui, au moment même où lui, Nicolas le croisait sur le chemin du retour. Sachant que leurs maisons sont distantes l'une de l'autre de 100 m, quelle distance sépare la boulangerie de la maison de Nestor ?

Un grand canal rectiligne passe entre deux villages, plus près de l'un que de l'autre. On veut y construire deux ponts perpendiculaires aux rives. Le premier sera tel que les deux villages soient à distance égale de l'entrée correspondante du pont ; le second tel que la route joignant les deux villages qui l'emprunte soit la plus courte possible.

Où doit-on construire les ponts ?

Un bateau se déplace sur une rivière dont le courant a une vitesse de 3 km/h. Il va tantôt dans un sens, tantôt dans l'autre. Il revient ainsi à son point de départ 6 heures après être parti, en ayant effectué un périple de 36 km.

Quelle est sa vitesse, sachant qu'il ne perd pas de temps en changeant de sens ?

Des enfants se partagent un sac de billes. Le premier enfant en prend 1 et le dixième de celles qui restent, puis le deuxième en prend 2 et le dixième du reste, le troisième 3 et le dixième du reste, et ainsi de suite jusqu'au dernier, qui prend tout ce qui reste. Combien y avait-il d'enfants et combien chacun a-t-il pris de billes sachant que toutes les parts étaient égales ?

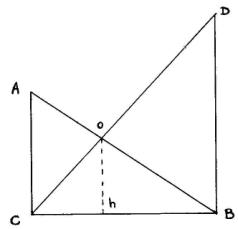
Calculer les longueurs DT et US

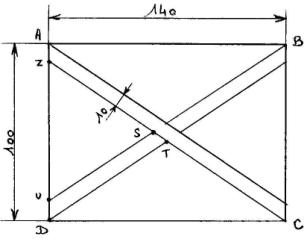
Sachant que : AB = 2, que CD = 3, et que OH = 1. Quelle est la valeur de CB ?

397 pions sont disposés sur une table, formant un hexagone régulier, comme sur le schéma.

Combien y a-t-il de pions sur chacun des 6 côtés.

Une roue à 8 dents s'engrène dans une autre à 24 dents. La petite roue tourne autour de la grosse. Combien de fois la petite roue aura-t-elle tourné autour de son axe lorsqu'elle aura effectué 3,5 tours complets de la grosse ?

L'autoroute Biarritz-Bilbao a pour longueur approximative 150 km. En Mercedes, Jean mets pour la franchir 25 minutes de moins que sa femme avec sa Clio. Or, l'autre jour, ils sont partis en même temps, elle de Bilbao et lui de Biarritz. Quand ils se sont croisés, ils ont observé que la différence entre les distances encore à franchir, en km, était égale à la différence entre les nombres de minutes qu'il leur restait encore à rouler, s'ils conservaient leurs vitesses habituelles respectives. A combien de km étaient-ils alors de Bilbao ? Et combien de temps avaient-ils roulé avant de se croiser ?

Deux paysannes ont apporté au marché ensemble 100 oeufs. L'une d'elle avait un plus grand nombre d’œufs que l'autre, mais toutes les deux ont reçu la même somme. La première a dit alors à la seconde : "Si j'avais eu tes oeufs, j'aurais reçu 15 francs". l'autre a répondu : "Et si moi, j'avais eu tes oeufs, j'aurais reçu 6 francs et 2/3".

Combien d’œufs avait chaque paysanne ?

Pour la somme de 50 francs on a acheté 100 fruits différents aux prix suivant :

Melons : 5 francs .........

Pommes : 1 franc .........

Prunes : 10 centimes.

Combien de fruits de chaque sorte ont été achetés ?

Quatre statues alimentent un bassin près du lac Léman. Chacune d'elles représente un des 4 grands fleuves qui prennent leur source en Suisse. C'est ainsi que le Pô remplit le bassin à lui tout seul en 4 jours, tandis qu'il faut 3 jours au Rhin, 2 au Danube, un au Rhône et 10 h 30 min. 40 sec aux 4 statues réunies.

En combien de temps, lorsqu'il cesse d'être alimenté, le bassin s'évapore-t-il ?

Un ascenseur est installé dans un immeuble de 100 étages. Il n'y a que deux boutons qui agissent. Si l'on presse le premier bouton l'ascenseur monte de 7 étages plus haut ; si l'on presse le second bouton il descend neuf étages plus bas.

Peut-on, en se servant de cet ascenseur se retrouver au 72ème étage en partant du premier ?

Un automate A multiplie un nombre donné par 3 pour 10 F. Un automate B, pour 1 F, ajoute 2 à un nombre donné.

Transformer à l'aide des automates A et B le nombre 0 en 1998 en dépensant dans cette opération une somme qui n'excède pas 55 F.

Quel est le plus petit nombre de poids nécessaire pour peser un nombre arbitraire de grammes de 1 à 1000 en se servant d'une balance à bascule (on peut mettre les poids sur n'importe lequel des plateaux de la balance) ?

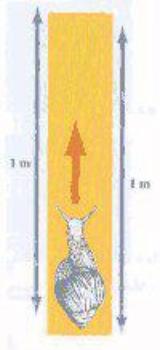
Un certain jour, quelques personnes ont observé un escargot pendant 10 heures. Chacune l'a observé une heure juste et a pu remarquer qu'il avait avancé de 1 mètre durant cette heure. L'escargot n'est jamais resté sans observateur.

Quelle est la plus grande distance que l'escargot a pu parcourir pendant ces 10 heures ?

Une cargaison de 13 500 kilos est mise en caisse ; le poids de chacune de ces caisses ne dépasse pas 350 kilos.

Démontrer que toute la cargaison peut être emportée par camion si chacun d'eux peut transporter tout au plus 1 500 kg.

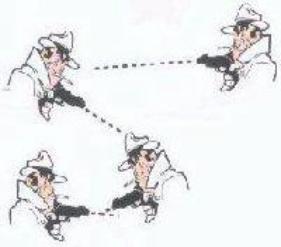
Sur la place de l'Hôtel de ville, 50 gangsters se sont rassemblés. Ils commencent à tirer l'un sur l'autre simultanément, chacun tirant sur le plus proche ou l'un des plus proches.

Quel est le nombre minimum de tués ?

Dans la forêt du baron de Feuilleverte il y a des bouleaux et des sapins ; on sait qu'à une distance de 1 km de tout sapin il y a exactement 10 bouleaux. Et pourtant le baron affirme que, dans sa forêt, il y a plus de sapins que de bouleaux.

Est-ce vraiment possible ?

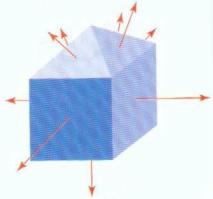
Soit un polyèdre convexe. On mène un vecteur perpendiculaire à chacune de ses faces et ayant une longueur égale à l'aire de cette face. Démontrer que la somme de ces vecteurs est égale au vecteur nul.

Un 400-gone régulier est découpé en parallélogrammes. Prouver que parmi ces parallélogrammes il existe au moins 100 rectangles.

Un tétraèdre se trouve à l'intérieur d'un autre tétraèdre. Est-ce que la somme des longueurs des arêtes de la pyramide intérieur peut être plus grande que celle de la pyramide extérieur.

Existe-t-il 1998 naturels consécutifs dont la somme soit le cube d'un entier naturel ?

Les cases d'un rectangle 5 41 sont peintes de deux couleurs. Démontrer que l'on peut choisir 3 lignes et 3 colonnes de sorte que les neuf case situées à leurs intersections soient de la même couleur.

Des points sont disposés sur une sphère. Ils commencent à se mouvoir avec des vitesses constantes et égales en valeur absolue (les uns vont dans le sens direct, les autre dans le sens rétrograde). S’étant heurté, deux points s'éloignent tout en conservant, en valeur absolue, leur vitesse initiale et en restant sur la même courbe.

Démontrer qu'il arrive un moment où tout point se trouve dans sa position initiale.